The Pooling Unit
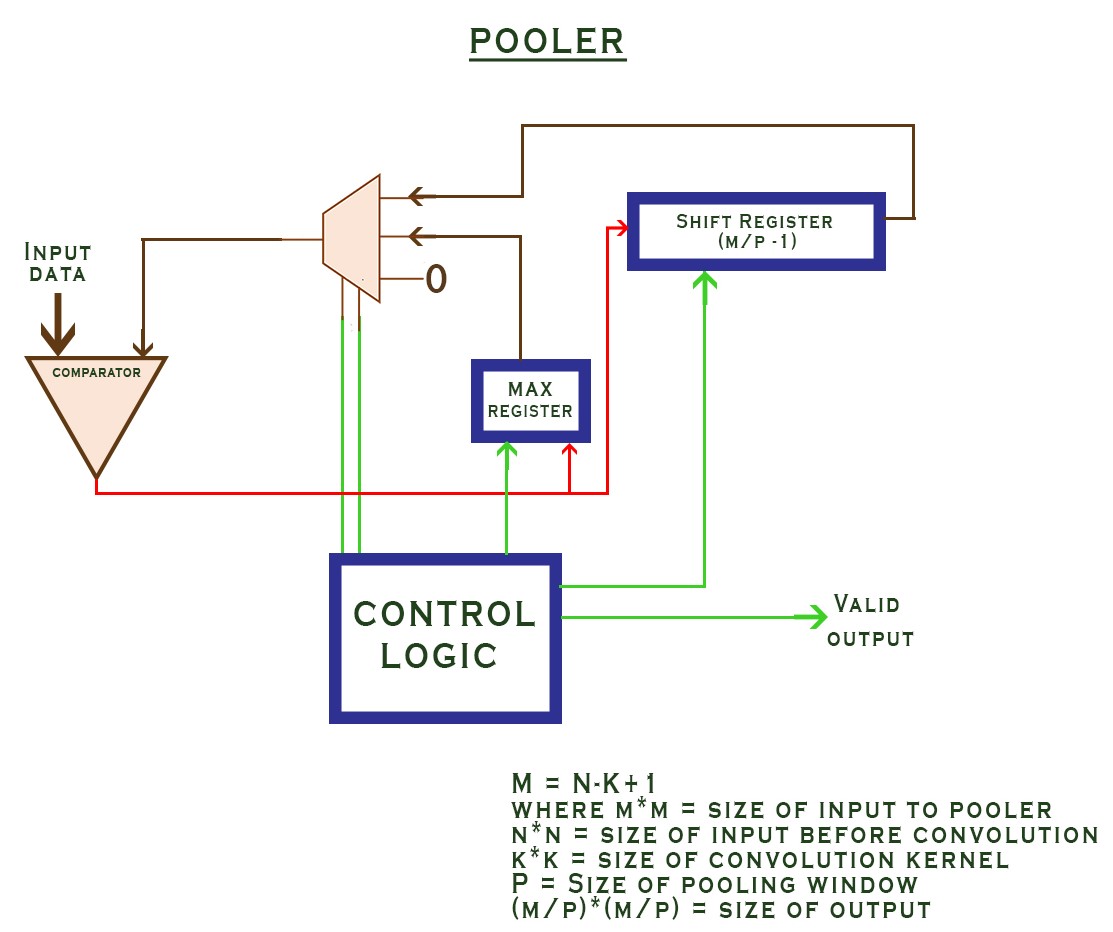
In this article we design a module that can very efficiently perform Max Pooling and Average pooling of an input matrix in Verilog HDL. This will go into our Deep Learning accelerator as mentioned in the previous articles in the series.
Part Zero - The Introduction
Part One - The Architecture Outline
Part Two - The Convolution Engine
Part Three - The Activation Function
Part Four - The Pooling Unit
Part Five - Adding fixed-point arithmetic to our design
Part Six - Putting it all together: The CNN Accelerator
Part Seven - System integration of the Convolution IP
Part Eight - Creating a multi-layer neural network in hardware.
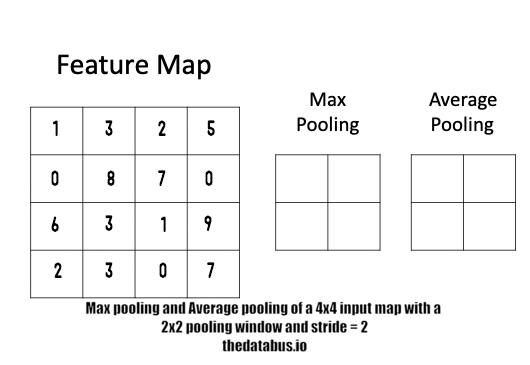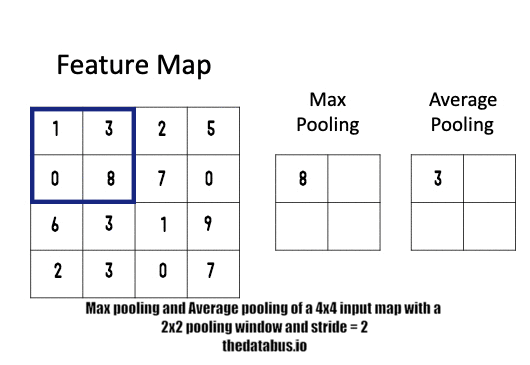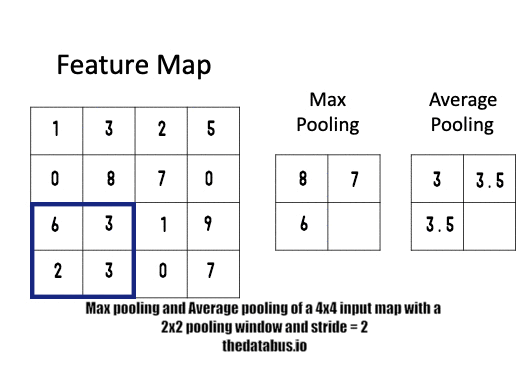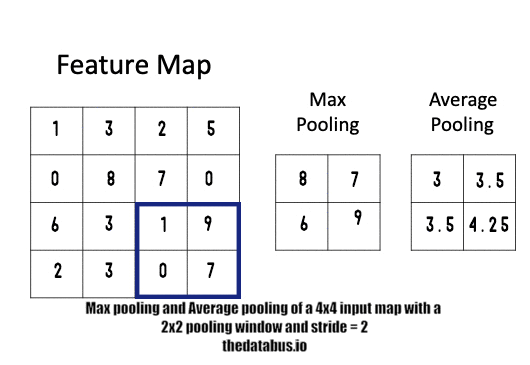
What is pooling?
The pooler is the part of this design that implements the Max Pooling operation. The animation below shows you what a max-pooling operation is. Basically, it is a particular method of down-sampling data at various stages of the Neural Network in order to reduce the number of parameters involved. this can serve as a good quick introduction to the mathematical process of pooling.
One design aspect that we need to keep in mind is that the pooler has also been designed in a pipelined streaming type of architecture in order to complement the Convolver. That is, data coming out of the convolver can be continuously fed into the pooler at every clock cycle and output shall appear after a certain number of clock cycles, this output will be a downsampled version of the input. i.e the output of the convolver.
Understandably, the output of the Max pooler shall be a fraction of the size of its input. This depends on how big the pooling window is. However, most of the commonly used neural networks do not have pooling windows larger than of dimensions 2X2 since anything bigger than that becomes too destructive an operation and results in significant loss of information.
Here is the code for the Max pooler: It is mostly a bunch of control statements that generate control signals for all the individual units in the pooler based on certain conditions that vary with the values of N, K, and P.
Code
NOTE: Currently this module only implements the max-pooling function since it is the most commonly used one in almost every neural network. However, average pooling is another scheme that is gaining popularity today. That too shall be implemented in the coming time.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83 | //file: pooler.v
//this is the top module of the pooling unit and it instantiates several sub-blocks which are explained further in the article
`timescale 1ns / 1ps
module pooler #(
parameter m = 9'h00c, //size of input image/activation map (post convolution)
parameter p = 9'h003, //size of pooling window
parameter N = 16, //total bitwidth of data
parameter Q = 12, //number of fractional bits in the Fixed Point representation
parameter ptype = 0, //ptype = 0 -> max pooling, ptype = 1 -> average pooling
parameter p_sqr_inv = 16'b0000010000000000 //this parameter is needed in average pooling case where the sum is divided by p**2.
//It needs to be supplied manually and should be equal to (1/p)^2 in whatever the
//(Q,N) format is being used.
)(
input clk,
input ce,
input master_rst,
input [N-1:0] data_in,
output [N-1:0] data_out,
output valid_op, //output signal to indicate the valid output
output end_op //output signal to indicate when all the valid outputs have been
//produced for that particular input matrix
);
wire rst_m,op_en,pause_ip,load_sr,global_rst;
wire [1:0] sel;
wire [N-1:0] comp_op;
wire [N-1:0] sr_op;
wire [N-1:0] max_reg_op;
wire [N-1:0] div_op;
wire ovr;
wire [N-1:0] mux_out;
wire temp2;
reg [N-1:0] temp;
control_logic2 #(m,p) log( //This block is the brains of this pooling unit. It generates
//the various signals needed to control all the other blocks
.clk(clk), //in the pooling unit.
.master_rst(master_rst),
.ce(ce),
.sel(sel),
.rst_m(rst_m),
.valid_op(valid_op),
.load_sr(load_sr),
.global_rst(global_rst),
.end_op(end_op)
);
comparator2 #(.N(N),.ptype(ptype)) cmp( //ptype = 0 -> This comparator outputs the maximum of
.ip1(data_in), //the two inputs.
.ip2(mux_out), //ptype = 1 -> This comparator outputs the sum of the
.comp_op(comp_op) //two inputs.
);
max_reg #(.N(N)) m1( //A simple register to hold the current maximum/sum
.clk(clk), //value. It can also be reset to zero
.din(comp_op),
.rst_m(rst_m),
.global_rst(temp2),
.master_rst(master_rst),
.reg_op(reg_op)
);
variable_shift_reg #(.WIDTH(N),.SIZE((m/p))) SR (
.d(comp_op), // input [N-1 : 0] d
.clk(clk), // input clk
.ce(load_sr), // input ce
.rst(global_rst && master_rst), // input sclr
.out(Q) // output [N-1 : 0] q
);
input_mux #(.N(N)) mux( //the multiplexer that controls one input of the
.ip1(Q), //comparator (refer post title image)
.ip2(reg_op),
.sel(sel),
.op(mux_out)
);
qmult #(N,Q) mul (max_reg_op,p_sqr_inv,div_op,ovr); //fixed point multiplier
assign data_out = ptype ? div_op : max_reg_op; //for average pooling, we output the sum divided by p**2
endmodule
|
Despite looking a bit taunting at first, most of the blocks in the above module are pretty simple and straight forward. Their operations are just as mentioned in the comment next to the module instantiation. I shall be skipping the code for these modules for brevity sakes. You can readily find all the code and test benches at the Github repo of this site.
However, the module that says control_logic2 is the most important sub-module of the pooling unit. It generates all the control signals shown in the title diagram of this page. These signals tell all the other modules in the pooling unit how to behave and what data to send where. It is very important that we dig deep into the functioning of this control logic module.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156 | //file: control_logic2.v
`timescale 1ns / 1ps
// The following are the various cases that arise as the pooling window moves over the input matrix
// each case requires a different kind of behaviour from the other modules in the pooler.
//NOTE: here 'max value' => maximum of all the values withing the pooling window
//1. normal case : just store the max value in the register.
//2. end of one neighbourhood: store the max value to the shift register.
//3. end of row: store the max value in the shift register and then load the max register from the shift register.
//4. end of neighbourhood in the last row: make output valid and store the max value in the max register.
//5. end of last neighbourhood of last row: make op valid and store the max value in the max register and then reset the entire module.
//SIGNALS TO BE HANDLED IN EACH CASE
//CASE 1 2 3 4 5
//1. load _sr low high high high low
//2. sel low low high high low
//3. rst_m low high low low low
//4. op_en low low low high high
//5. global_rst low low low low high
module control_logic(
input clk, //clock
input master_rst, //reset to initialize every module
input ce, //clock-enable
output reg [1:0] sel, //selection output that connects to the multiplexer input select lines
output reg rst_m, //signal to reset the maximum register
output reg op_en, //signal to tell the outside world when the output is valid
output reg load_sr, //signal to enable the clock for the shift register
output reg global_rst, //signal to reset all the othe modules except the control_logic
output reg end_op //signal to indicate end of all outputs for a particular input matrix
);
parameter m = 9'h004; //size of input matrix is m X m
parameter p = 9'h002; //size of the pooilng window is p X p
integer row_count =0; //the entire module works based on the row and column counters
integer col_count =0; //that tell it where exactly the window is at each clock cycle
integer count =0; //the master counter that increments and resets row_count and col_count
integer nbgh_row_count; //this counter keeps track of the number of neighbourhoods (pooling windows) completed
always@(posedge clk) begin
if(master_rst) begin
sel <=0;
load_sr <=0;
rst_m <=0;
op_en <=0;
global_rst <=0;
end_op <=0;
end
else begin
if(((col_count+1)%p !=0)&&(row_count == p-1)&&(col_count == p*count+ (p-2))&&ce) //op_en
begin
op_en <=1;
end
else begin
op_en <=0;
end
if(ce)
begin
if(nbgh_row_count == m/p) //end_op
begin
end_op <=1;
end
else
begin
end_op <=0;
end
if(((col_count+1) % p != 0)&&(col_count == m-2)&&(row_count == p-1)) //global_rst and pause_ip
begin
global_rst <= 1; // (reset everything)
end
else
begin
global_rst <= 0;
end
//end
if((((col_count+1) % p == 0)&&(count != m/p-1)&&(row_count != p-1))||((col_count == m-1)&&(row_count == p-1))) //rst_m
begin
rst_m <= 1;
end
else
begin
rst_m <= 0;
end
if(((col_count+1) % p != 0)&&(col_count == m-2)&&(row_count == p-1))
begin
sel <= 2'b10;
end
else
begin
if((((col_count) % p == 0)&&(count == m/p-1)&&(row_count != p-1))|| (((col_count) % p == 0)&&(count != m/p-1)&&(row_count == p-1))) begin //sel
sel<=2'b01;
end
else
begin
sel <= 2'b00;
end
end
if((((col_count+1) % p == 0)&&((count == m/p-1)))||((col_count+1) % p == 0)&&((count != m/p-1))) //load_sr
begin
load_sr <= 1;
end
else
begin
load_sr <= 0;
end
end
end
end
always@(posedge clk) begin //counters
if(master_rst) begin
row_count <=0;
col_count <=32'hffffffff;
count <=32'hffffffff;
nbgh_row_count <=0;
end
else
begin
if(ce)
begin
if(global_rst)
begin
row_count <=0;
col_count <=32'h0;
count <=32'h0;
nbgh_row_count <= nbgh_row_count + 1'b1;
end
else
begin
if(((col_count+1) % p == 0)&&(count == m/p-1)&&(row_count != p-1)) //col_count and row_count
begin
col_count <= 0;
row_count <= row_count + 1'b1;
count <=0;
end
else
begin
col_count<=col_count+1'b1;
if(((col_count+1) % p == 0)&&(count != m/p-1))
begin
count <= count+ 1'b1;
end
end
end
end
end
end
endmodule
|
Simulation
The following code presents a very minimalistic test-bench to check the working of the pooler. This test bench has been far extended to cover all possible inputs and can be found in the Github Repo
The test-bench here applies a 2X2 pooling window on the following 4X4 input matrix:
| +-----------+
|00|01|02|03|
+-----------+
|04|05|06|07|
+-----------+
|08|09|10|11|
+-----------+
|12|13|14|15|
+-----------+
|
You can easily guess what the output matrix should look like:
| +-----+
|05|07|
+-----+
|13|15|
+-----+
|
Let's see if our design is working!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 | //file: pooler_tb.v
`timescale 1ns / 1ps
module pooler_tb();
reg clk,ce;
reg [31:0] data_in;
reg master_rst;
wire [31:0] data_out;
wire valid_op;
wire end_op;
parameter clkp = 40;
integer i;
pooler #(9'h4,9'h2) dut(
.clk(clk),
.ce(ce),
.master_rst(master_rst),
.data_in(data_in),
.data_out(data_out),
.valid_op(valid_op),
.end_op(end_op)
);
initial
begin
clk = 0;
ce = 0;
data_in = 0;
master_rst = 0;
#100;
master_rst = 1;
#clkp;
master_rst = 0;
#10;
ce = 1;
for(i = 0; i<25;i = i+1)
begin
data_in = i;
#clkp;
end
end
always #(clkp/2) clk = ~clk;
endmodule
|
On simulating this test-bench on xilinx vivado, we get the following result:

As is visible, the valid_op signal goes high only at the correct outputs. i.e the maximum values in the window
All the design files along with their test benches can be found at the Github Repo
PREVIOUS:The architecture outline
NEXT:Adding fixed point arithmetic to your design


